Dynamic Connectivity & Disjoint Sets
Given \(N\) nodes, some connected amongst themselves, does a path exist between any two given nodes?
The connectivity relationship leads to equivalence classes. We call these classes connected components. Any two nodes in a connected component are connected (although not necessarily directly).
We primarily want to check for connectedness (find), and perform unions of connected components (i.e. connect an object from one component to an object from a different component).
As equivalence classes are disjoint, this algorithm is also useful for checking membership of 2 elements in a collection of disjoint sets.
Algorithms
These algorithms merely test for connectedness. They do not give the path connecting the two nodes.
Quick Find
Take an array A of size \(N\). The index of the array represents each node. Let all connected nodes share the same value, but different connected components have distinct values.
So A[3]=4 and A[7]=4 means that objects 3 and 7 are connected. Any index whose value is 4 is connected to these.
So checking for connectedness is \(O(1)\). However, constructing by multiple unions is \(O(N^{2})\) (as union is \(O(N)\)).
Quick Union
Here we construct the graph as a tree. Initially all nodes are disconnected, and we set their root to be themselves. If we connect two nodes, then we set the root of one node to be the same as the root of the other node. Note:
- By root I do not mean parent.
- As described above, the union is asymmetric. You’ll get different trees if you switch the order of your union (union(1, 4) vs union(4, 1)).
- The node that is the root is not really special in any way. We’ll exploit this later on.
Take an array A of size \(N\). The index of the array represents each node. The value represents the node’s parent.
To perform a find, check if the two elements share the same root.
To perform a union, make one’s root the child of the other’s root (so now they share the same root).
Complexity: If you end up with a really tall tree, both find and union are \(O(n)\).
Weighted Quick Union
This is similar to quick union, but now you ensure that when performing a union, you connect the root of the smaller tree to the root of the larger one.
This guarantees that the tree will never have depth greater than \(\lg N\). The reason is that whenever you do a union, you are increasing the depth by 1, but the smaller tree that contains the node at least doubles in size. You cannot double more than \(\lg N\) times.
So now find and union are at most \(O(\lg N)\).
An alternative way to weight it is by height of the tree (as opposed to number of nodes in the tree).
Path Compression
We can balance the tree even further. Given any node, you must traverse a number of nodes to get to the root. Keep a track of those nodes, and set their parents to be the root!
If you don’t want to traverse the path twice, just set each node in the path to have its grandparent as a parent.
Theory
There is no algorithm that always generates the graph in linear time, but one is close in practice.
Python Implementation
Quick Find
class QuickFind(object):
def __init__(self, N):
self.lst = range(N)
def find(self, a, b):
return self.lst[a] == self.lst[b]
def union(self, a, b):
old = self.lst[a]
new = self.lst[b]
for ind, x in enumerate(self.lst):
if x == old:
self.lst[ind] = new
Quick Union
class QuickUnion(object):
def __init__(self, N):
self.lst = range(N)
def get_root(self, ind):
while ind != self.lst[ind]:
ind = self.lst[ind]
return ind
def find(self, a, b):
return self.get_root(a) == self.get_root(b)
def union(self, a, b):
root_a = self.get_root(a)
self.lst[root_a] = self.get_root(b)
Weighted Quick Union
class WeightedQuickUnion(object):
def __init__(self, N):
self.lst = range(N)
self.sizes = [1] * N
def get_root(self, ind):
while ind != self.lst[ind]:
ind = self.lst[ind]
return ind
def find(self, a, b):
return self.get_root(a) == self.get_root(b)
def union(self, a, b):
if self.sizes[self.get_root(a)] < self.sizes[self.get_root(b)]:
self.lst[self.get_root(a)] = self.get_root(b)
self.sizes[self.get_root(b)] += self.sizes[self.get_root(a)]
else:
self.lst[self.get_root(b)] = self.get_root(a)
self.sizes[self.get_root(a)] += self.sizes[self.get_root(b)]
Compressed Quick Union
class CompressedQuickUnion(object):
def __init__(self, N):
self.lst = range(N)
def get_root(self, ind):
seen = set([])
while ind != self.lst[ind]:
seen.add(ind)
ind = self.lst[ind]
root = ind
# Point all parents in the path I just traversed to the root.
for x in seen:
self.lst[x] = root
return root
def find(self, a, b):
return self.get_root(a) == self.get_root(b)
def union(self, a, b):
root_a = self.get_root(a)
self.lst[root_a] = self.get_root(b)
Compressed Quick Union One Pass
class CompressedQuickUnionOnePass(object):
def __init__(self, N):
self.lst = range(N)
def get_root(self, ind):
seen = set([])
while ind != self.lst[ind]:
# Point to the grandparent. This will always work as the
# root points to itself.
self.lst[ind] = self.lst[self.lst[ind]]
ind = self.lst[ind]
return ind
def find(self, a, b):
return self.get_root(a) == self.get_root(b)
def union(self, a, b):
root_a = self.get_root(a)
self.lst[root_a] = self.get_root(b)
Weighted Compressed Quick Union
class WeightedCompressedQuickUnion(object):
def __init__(self, N):
self.lst = range(N)
self.sizes = [1] * N
def get_root(self, ind):
seen = set([])
while ind != self.lst[ind]:
seen.add(ind)
ind = self.lst[ind]
root = ind
# Point all parents in the path I just traversed to the root.
for x in seen:
self.lst[x] = root
return root
def find(self, a, b):
return self.get_root(a) == self.get_root(b)
def union(self, a, b):
if self.sizes[self.get_root(a)] < self.sizes[self.get_root(b)]:
self.lst[self.get_root(a)] = self.get_root(b)
self.sizes[self.get_root(b)] += self.sizes[self.get_root(a)]
else:
self.lst[self.get_root(b)] = self.get_root(a)
self.sizes[self.get_root(a)] += self.sizes[self.get_root(b)]
Performance
For each \(N\), I started off with an originally disconnected set and performed \(N\) unions (randomly). In the plots below, I divide the run time by \(N\) to “normalize it”, so it shows the time to do a single union/find for a graph of size \(N\).
Unions:
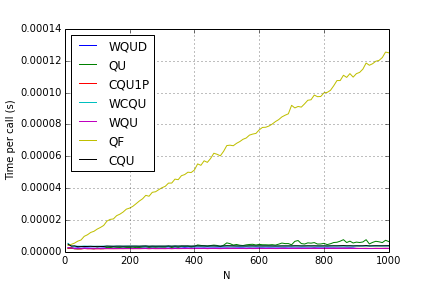
All Unions Without Quick Find:
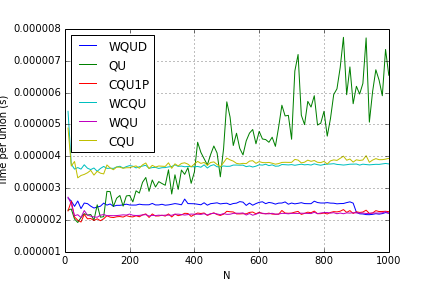
Finds:
C++ Implementation
unionfind.h:
class UnionFind
{
protected:
std::vector<unsigned int> indices;
public:
virtual bool find(unsigned int a, unsigned int b) const = 0;
virtual void make_union(unsigned int a, unsigned int b) = 0;
UnionFind(unsigned int N);
};
class QuickFind : public UnionFind
{
private:
public:
bool find(unsigned int a, unsigned int b) const;
void make_union(unsigned int a, unsigned int b);
QuickFind(unsigned int N) : UnionFind(N) {}
};
class QuickUnion : public UnionFind
{
protected:
unsigned int get_root(unsigned int ind) const;
public:
bool find(unsigned int a, unsigned int b) const;
void make_union(unsigned int a, unsigned int b);
QuickUnion(unsigned int N) : UnionFind(N) {}
};
class WeightedQuickUnion : public QuickUnion
{
protected:
std::vector<unsigned int> sizes;
public:
void make_union(unsigned int a, unsigned int b);
WeightedQuickUnion(unsigned int N) : QuickUnion(N)
{
sizes.assign(N, 1);
}
};
// Same as WeightedQuickUnion but the sizes vector contains the depth of the
// tree.
class WeightedQuickUnionDepth : public WeightedQuickUnion
{
public:
void make_union(unsigned int a, unsigned int b);
WeightedQuickUnionDepth(unsigned int N) : WeightedQuickUnion(N)
{
}
};
class CompressedQuickUnion : public QuickUnion
{
protected:
unsigned int get_root(unsigned int ind);
public:
CompressedQuickUnion(unsigned int N) : QuickUnion(N) {}
};
class CompressedQuickUnionOnePass : public QuickUnion
{
protected:
unsigned int get_root(unsigned int ind);
public:
CompressedQuickUnionOnePass(unsigned int N) : QuickUnion(N) {}
};
class WeightedCompressedQuickUnion : public CompressedQuickUnion
{
protected:
std::vector<unsigned int> sizes;
public:
void make_union(unsigned int a, unsigned int b);
WeightedCompressedQuickUnion(unsigned int N) : CompressedQuickUnion(N)
{
sizes.assign(N, 1);
}
};
unionfind.cpp:
#include <vector>
#include <set>
#include "unionfind.h"
UnionFind::UnionFind(unsigned int N)
{
indices.resize(N);
for(std::vector<unsigned int>::size_type i = 0; i != indices.size(); i++)
{
indices[i] = i;
}
}
bool QuickFind::find(unsigned int a, unsigned int b) const
{
return indices[a] == indices[b];
}
void QuickFind::make_union(unsigned int a, unsigned int b)
{
unsigned int old = indices[a];
unsigned int New = indices[b];
for(std::vector<unsigned int>::iterator it = indices.begin();
it != indices.end(); ++it)
{
if (*it == old)
{
*it = New;
}
}
}
unsigned int QuickUnion::get_root(unsigned int ind) const
{
while (ind !=indices[ind]) {
ind = indices[ind];
}
return ind;
}
bool QuickUnion::find(unsigned int a, unsigned int b) const
{
return get_root(a)==get_root(b);
}
void QuickUnion::make_union(unsigned int a, unsigned int b)
{
indices[get_root(a)] = indices[get_root(b)];
}
void WeightedQuickUnion::make_union(unsigned int a, unsigned int b)
{
unsigned int root_a = get_root(a);
unsigned int root_b = get_root(b);
if (sizes[root_a] < sizes[root_b])
{
indices[root_a] = root_b;
sizes[root_b] += sizes[root_a];
}
else
{
indices[root_b] = root_a;
sizes[root_a] += sizes[root_b];
}
}
void WeightedQuickUnionDepth::make_union(unsigned int a, unsigned int b)
{
unsigned int root_a = get_root(a);
unsigned int root_b = get_root(b);
if (sizes[root_a] < sizes[root_b])
{
indices[root_a] = root_b;
}
else if (sizes[root_a] > sizes[root_b])
{
indices[root_b] = root_a;
}
else
{
indices[root_a] = root_b;
sizes[root_b] += 1;
}
}
unsigned int CompressedQuickUnion::get_root(unsigned int ind)
{
std::set<unsigned int> seen;
while (ind !=indices[ind]) {
seen.insert(ind);
ind = indices[ind];
}
unsigned int root = ind;
for (std::set<unsigned int>::iterator iter=seen.begin();
iter != seen.end(); ++iter)
{
indices[*iter] = root;
}
return root;
}
unsigned int CompressedQuickUnionOnePass::get_root(unsigned int ind)
{
while (ind !=indices[ind]) {
indices[ind] = indices[indices[ind]];
ind = indices[ind];
}
return ind;
}
void WeightedCompressedQuickUnion::make_union(unsigned int a, unsigned int b)
{
unsigned int root_a = get_root(a);
unsigned int root_b = get_root(b);
if (sizes[root_a] < sizes[root_b])
{
indices[root_a] = root_b;
sizes[root_b] += sizes[root_a];
}
else
{
indices[root_b] = root_a;
sizes[root_a] += sizes[root_b];
}
}
Performance
For each \(N\), I started off with an originally disconnected set and performed \(N\) unions (randomly). In the plots below, I divide the run time by \(N\) to “normalize it”, so it shows the time to do a single union/find for a graph of size \(N\).
Unions:
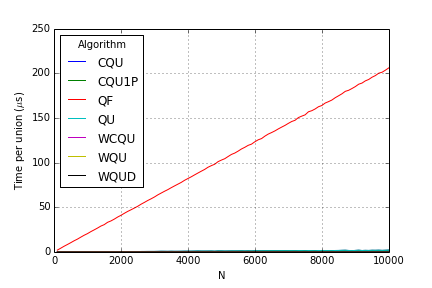
All Unions Without Quick Find:
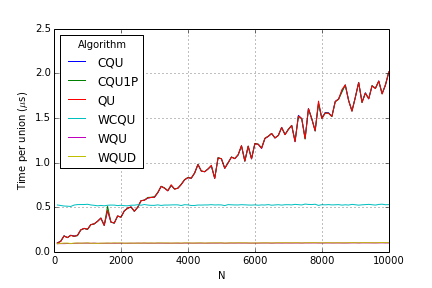
These results differ from my Python implementation somewhat. While weighting really showed improvements over quick union, compression had virtually no effect!
Finds:
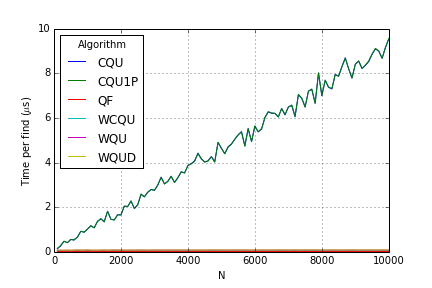
CQU, CQU1P and QU are almost identical, which does not seem right at all! It’s as if compression had no effect.
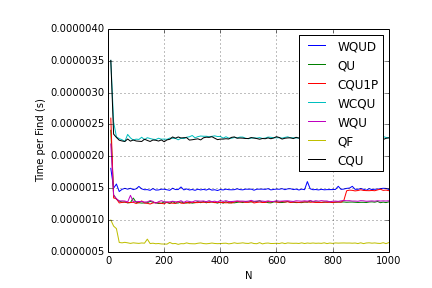
Finds without CQU, CQU1P and QU: