Trigonometric Identities

Formula for \(\cos(\alpha-\beta)\)

Consider the unit circle below:

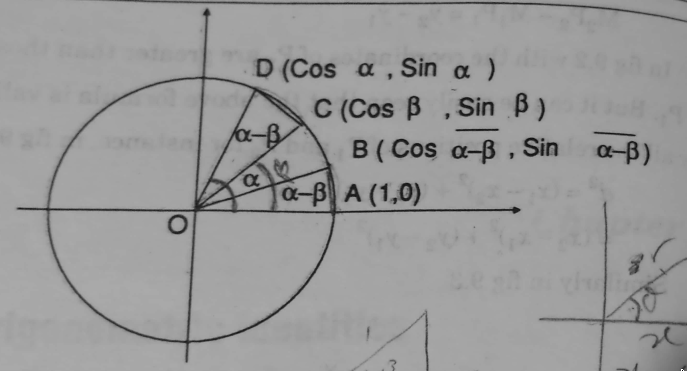
Here, we make \(\overline{AB}=\overline{CD}\), so they have the same angles.

Since we made the lengths the same, lets actually calculate the lengths using the coordinates.

Expand these and use \(\sin^{2}x+\cos^{2}x=1\) and you’ll eventually get:

In Sage:

x, y = var('x y')
print((cos(x-y)).trig_expand())

cos(x)*cos(y) + sin(x)*sin(y)

All the Other Identities

1. \(\cos(-\alpha)=\cos\alpha\)
2. \(\cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha\)
3. \(\cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha\)
4. \(\sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha\)
5. \(\sin(-\alpha)=-\sin\alpha\)
6. \(\tan(-\alpha)=-\tan\alpha\)
7. \(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
8. \(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\)
9. \(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
10. \(\sin(\pi-\beta)=\sin\beta\)
11. \(\cos(\pi-\beta)=-\cos\beta\)
12. \(\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\)
13. \(\sin2\alpha=2\sin\alpha\cos\alpha\)
14. \(\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha=2\cos^{2}\alpha-1=1-2\sin^{2}\alpha\)
15. \(\tan2\alpha=\frac{2\tan\alpha}{1-\tan^{2}\alpha}\)
16. \(\sin\alpha=\pm\sqrt{\frac{1-\cos2\alpha}{2}}\)
17. \(\cos\alpha=\pm\sqrt{\frac{1+\cos2\alpha}{2}}\)
18. \(\tan\alpha=\pm\sqrt{\frac{1-\cos2\alpha}{1+\cos2\alpha}}\)
19. \(\sin A+\sin B=2\sin\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right)\)
20. \(\sin A-\sin B=2\sin\left(\frac{A-B}{2}\right)\cos\left(\frac{A+B}{2}\right)\)
21. \(\cos A+\cos B=2\cos\left(\frac{A+B}{2}\right)\cos\left(\frac{A-B}{2}\right)\)
22. \(\cos A-\cos B=2\sin\left(\frac{A+B}{2}\right)\sin\left(\frac{A-B}{2}\right)\)