We introduced 2-3 trees with highly desirable properties. Here we’ll convert them into binary trees while maintaining all the desirable properties.
We need a way to convert a 3-node into something that makes sense in binary trees. Here’s how:
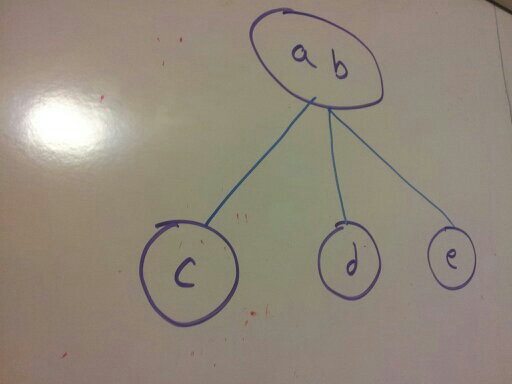
becomes
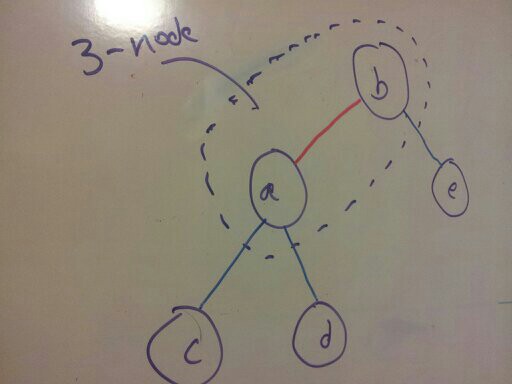
Note that the color between nodes “a” and “b” is red. Red links are only internal links in 3-nodes. All other links are black (blue in my diagrams).
Properties
- No node can have two red links.
- A path from the root to the null will always have the same number of black links. Thus, the tree is “black balanced”.
- By convention, red links will always be on the left.
- The height of the tree is upper bounded by double the black only path. It is upper bounded by \(2\lg N\). In practice, it is usually closer to the optimal value!
Operations
Many of our operations ignore the color of the edges. The main benefit of this tree is that it is relatively balanced.
Search
We search just as we would a regular binary search tree - completely ignoring the color.
Left Rotation
Convert a right leaning red link to lean left.
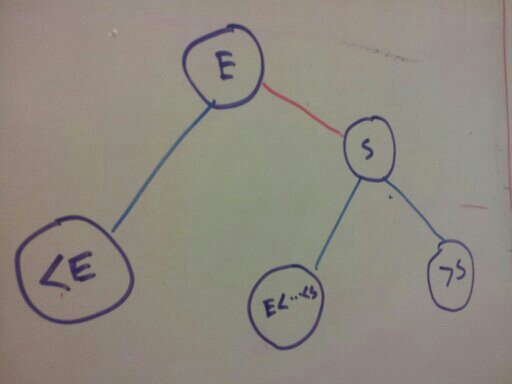
becomes
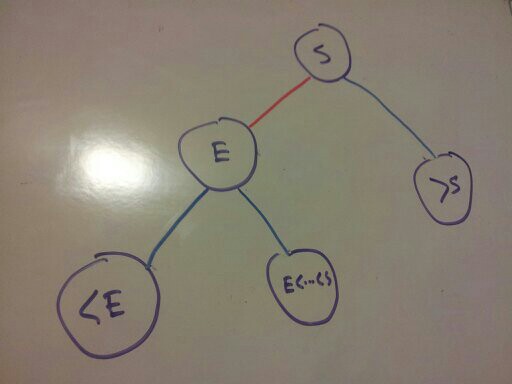
Right Rotation
Opposite of left rotation.
Converting a 4-node into a 3-node
This is done by making both its left and right edges black (from red). We must check that its parent edge is not red, though. After the transformation, the parent’s edge becomes red. This may cause this to be a right leaning 3-node, at which point we do a left rotation.
Insertion
Conceptually, do the insertion as you would in a 2-3 tree, coloring links appropriately, and performing rotations as needed. We can itemize all the possibilities, but in the end, the logic reduces to a few simple rules (applied in this order):
- If the right edge is red and the left edge is black, rotate left.
- If the left edge and its left edge are black, rotate right.
- If both the left and right edges are red, flip colors (convert a 4-node into a 3-node).
Deletion
This is a bit complicated and I omitted it.
Implementations In Code
Python
from Queue import Queue
class Node:
def __init__(self, key, value, color):
"""
color is "R" for red and "B" for black.
"""
self.key = key
self.value = value
self.left = None
self.right = None
self.size = 1
if color.upper() not in ("R", "B"):
raise ValueError
self.color = color.upper()
def get_min(self):
""" Return the node with the min key. """
if not self.left:
return self
node = self
while node.left:
node = node.left
return node
def get_max(self):
""" Return the node with the max key. """
if not self.right:
return self
node = self
while node.right:
node = node.right
return node
def rotate_left(node):
"""
node's right link is red. Reorient things so that the node's left
link is red. Returns the right node (useful in "rebuilding" the tree).
"""
assert is_red(node.right)
new_left_size = node.size - node.right.size + size(node.right.left)
new_right_size = node.size
right_node = node.right
node.right = right_node.left
right_node.left = node
right_node.color = node.color
node.color = "R"
node.size = new_left_size
right_node.size = new_right_size
return right_node
def rotate_right(node):
"""
node's right link is red. Reorient things so that the node's left
link is red. Returns the right node (useful in "rebuilding" the tree).
"""
assert is_red(node.left)
new_right_size = node.size - node.left.size + size(node.left.right)
new_left_size = node.size
left_node = node.left
node.left = left_node.right
left_node.right = node
left_node.color = node.color
node.color = "R"
node.size = new_right_size
left_node.size = new_left_size
return left_node
def flip_colors(node):
"""
Used when converting a 4-node into a 3-node
"""
assert not is_red(node)
assert is_red(node.left)
assert is_red(node.right)
node.color = "R"
node.left.color = "B"
node.right.color = "B"
def is_red(node):
"""
Checks if a link to a node's parent is red or black. A null node by
convention has a black link.
"""
if not node:
return False
return (node.color == "R")
def size(node):
if node:
return node.size
else:
return 0
class RedBlackTree:
def __init__(self, root):
self.root = root
def insert(self, key, value):
self.root = self.__doinsert(self.root, key, value)
# Sometimes in flipping the root's color changes. The root's
# color should always be black!
self.root.color = "B"
def __doinsert(self, node, key, value):
if not node:
return Node(key, value, "R")
if key < node.key:
node.left = self.__doinsert(node.left, key, value)
node.size += 1
elif key > node.key:
node.right = self.__doinsert(node.right, key, value)
node.size += 1
else:
node.value = value
if is_red(node.right) and not is_red(node.left):
node = rotate_left(node)
if is_red(node.left) and is_red(node.left.left):
node = rotate_right(node)
if is_red(node.right) and is_red(node.left):
flip_colors(node)
return node
def search(self, key):
"""
Searches the tree for a node with that key. If it finds one, it
returns the node.
"""
node = self.root
while node:
if key == node.key:
return node
if key < node.key:
node = node.left
else:
node = node.right
return node
def __getfloor(self, node, key):
if not node:
return None
if node.key == key:
return node
if key < node.key:
return self.__getfloor(node.left, key)
if key > node.key:
n = self.__getfloor(node.right, key)
if n: # Found it in the right subtree.
return n
else: # Nothing smaller in the right subtree.
return node
def floor(self, key):
""" Return the largest key smaller than or equal to key. """
return self.__getfloor(self.root, key)
def ceiling(self, key):
""" Return the smallest key larger than or equal to key. """
return self.__getceiling(self.root, key)
def __getceiling(self, node, key):
if not node:
return None
if node.key == key:
return node
if key > node.key:
return self.__getceiling(node.right, key)
if key < node.key:
n = self.__getceiling(node.left, key)
if n: # Found it in the right subtree.
return n
else: # Nothing smaller in the right subtree.
return node
def rank(self, k):
""" How many keys less than k? """
return self.__getrank(self.root, k)
def __getrank(self, node, k):
if not node:
return 0
if k < node.key:
return self.__getrank(node.left, k)
if k > node.key:
# 1 is for current node which is smaller
return 1 + size(node.left) + self.__getrank(node.right, k)
if k == node.key:
if node.left:
return node.left.size
else:
return 0
def traverse(self):
q = Queue()
self.__inorder(self.root, q)
return q
def __inorder(self, node, queue):
if not node:
return
self.__inorder(node.left, queue)
queue.put(node)
self.__inorder(node.right, queue)
C++
#include <cstddef> // For NULL definition.
#include <queue>
#include <assert.h>
enum NodeColor {RED, BLACK};
class Node;
class Node
{
public:
int key;
int value;
Node* left;
Node* right;
int size;
NodeColor color;
Node(int key, int val, NodeColor color);
Node* get_min();
Node* get_max();
};
Node::Node(int key, int val, NodeColor color) : key(key), value(val), size(1),
left(NULL), right(NULL),
color(color) {}
Node* Node::get_min()
{
if(NULL == left)
{
return this;
}
Node* node = this;
while (NULL != node->left)
{
node = node->left;
}
return node;
}
Node* Node::get_max()
{
if(NULL == right)
{
return this;
}
Node* node = this;
while (NULL != node->right)
{
node = node->right;
}
return node;
}
int size(Node const * node)
{
if(NULL != node)
{
return node->size;
}
return 0;
}
// bool is_red(Node const * node);
bool is_red(Node const * node)
{
if (NULL == node)
{
return false;
}
return (node->color == RED);
}
// Node* rotate_left(Node* node);
Node* rotate_left(Node* node)
{
assert(is_red(node->right));
int new_left_size = node->size - node->right->size + size(node->right->left);
int new_right_size = node->size;
Node* right_node = node->right;
node->right = right_node->left;
right_node->left = node;
right_node->color = node->color;
node->color = RED;
node->size = new_left_size;
right_node->size = new_right_size;
return right_node;
}
// Node* rotate_right(Node* node);
Node* rotate_right(Node* node)
{
assert(is_red(node->left));
int new_right_size = node->size - node->left->size + size(node->left->right);
int new_left_size = node->size;
Node* left_node = node->left;
node->left = left_node->right;
left_node->right = node;
left_node->color = node->color;
node->color = RED;
node->size = new_right_size;
left_node->size = new_left_size;
return left_node;
}
void flip_colors(Node* node)
{
assert(!is_red(node));
assert(is_red(node->left));
assert(is_red(node->right));
node->color = RED;
node->left->color = BLACK;
node->right->color = BLACK;
}
class RedBlackTree
{
public:
Node* root;
RedBlackTree(Node* root);
~RedBlackTree();
void insert(int key, int value);
Node* floor(int key) const;
Node* ceiling(int key) const;
Node* search(int key);
int rank(int key) const;
std::queue<Node*> traverse() const;
private:
Node* doinsert(Node* node, int key, int value);
Node* getfloor(Node* node, int key) const;
Node* getceiling(Node* node, int key) const;
int getrank(Node* node, int key) const;
void inorder(Node* node, std::queue<Node*>& queue) const;
};
RedBlackTree::RedBlackTree(Node* root) : root(root) {}
Node* RedBlackTree::doinsert(Node* node, int key, int value)
{
if (NULL==node)
{
Node* newnode = new Node(key, value, RED);
return newnode;
}
if (key < node->key)
{
node->left = doinsert(node->left, key, value);
++(node->size);
}
else if (key > node->key)
{
node->right = doinsert(node->right, key, value);
++(node->size);
}
else
{
node->value = value;
}
if(is_red(node->right) && (!is_red(node->left)))
{
node = rotate_left(node);
}
if(is_red(node->left) and is_red(node->left->left))
{
node = rotate_right(node);
}
if(is_red(node->right) and is_red(node->left))
{
flip_colors(node);
}
return node;
}
void RedBlackTree::insert(int key, int value)
{
root = doinsert(root, key, value);
root->color = BLACK;
}
Node* RedBlackTree::search(int key)
{
Node* node = root;
while(NULL != node)
{
if(key == node->key)
{
return node;
}
else if(key < node->key)
{
node = node->left;
}
else if(key > node->key)
{
node = node->right;
}
}
return node;
}
Node* RedBlackTree::getfloor(Node* node, int key) const
{
if (NULL == node)
{
return NULL;
}
if(key == node->key)
{
return node;
}
if(key < node->key)
{
return getfloor(node->left, key);
}
if(key > node->key)
{
Node* n = getfloor(node->right, key);
if (NULL != n)
{
return n;
}
else
{
return node;
}
}
}
Node* RedBlackTree::floor(int key) const
{
return getfloor(root, key);
}
Node* RedBlackTree::getceiling(Node* node, int key) const
{
if (NULL == node)
{
return NULL;
}
if(key == node->key)
{
return node;
}
if(key > node->key)
{
return getceiling(node->right, key);
}
if(key < node->key)
{
Node* n = getceiling(node->left, key);
if (NULL != n)
{
return n;
}
else
{
return node;
}
}
}
Node* RedBlackTree::ceiling(int key) const
{
return getceiling(root, key);
}
int RedBlackTree::rank(int key) const
{
return getrank(root, key);
}
int RedBlackTree::getrank(Node* node, int key) const
{
if (NULL == node)
{
return 0;
}
if(key < node->key)
{
return getrank(node->left, key);
}
if(key > node->key)
{
return 1 + size(node->left) + getrank(node->right, key);
}
if(key == node->key)
{
if (NULL != node->left)
{
return node->left->size;
}
else
{
return 0;
}
}
}
void RedBlackTree::inorder(Node* node, std::queue<Node*>& queue) const
{
if (NULL == node)
return;
inorder(node->left, queue);
queue.push(node);
inorder(node->right, queue);
}
std::queue<Node*> RedBlackTree::traverse() const
{
std::queue<Node*> queue;
inorder(root, queue);
return queue;
}
// Not exactly the fastest way of doing things!
RedBlackTree::~RedBlackTree()
{
std::queue<Node*> queue = traverse();
while(!queue.empty())
{
Node* node = queue.front();
queue.pop();
node->left = NULL;
node->right = NULL;
delete node;
node = NULL;
}
}