Consider an \(N\times N\) square grid, where all the grids are black. Now let each square in the grid be white with probability \(p\). Does there exist a path from the bottom of this grid to the top by traversing only white squares?
This is a general problem. For example, if white represents a porous cell, then if such a path exists, one can have water flow from one end to the other. A similar model applies to phase transitions, etc.
To model this, instead of searching whether each square in the bottom is connected to each square in the top (an \(N^{2}\) operation), let there exist two invisible white cells - one beneath the bottom grid, and one above the top grid. Let the bottom invisible grid be connected to all the white grids in the bottom row, and likewise for the top. Then we need only check for connectedness amongst the invisible cells.
It turns out that for large enough \(N\), there is a sharp transition from opaque to percolated at around \(p=0.593\).
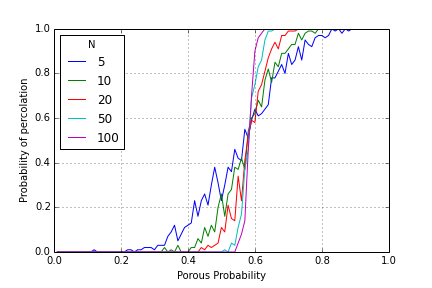
I calculated this in a naive manner: For each \(p\), I created a grid of size \(N\) about a 100 times and checked how many percolated. The ratio gives the percolation probability. Hence the curves not being smooth.
If we merely want to estimate the probability that yields percolation, we can run a Monte Carlo simulation. Create a grid, and continue to randomly set cells as white until percolation occurs. The percentage of white cells is a good measure of the percolation probability.
Code to generate plot:
#include <vector>
#include <iostream>
#include <cstdlib>
#include "unionfind.cpp"
#include <fstream>
// Get neighbors' indices for cell i in an NxN grid. We only care to return
// neighbors to the right and above us as we'll already have covered those
// before us.
std::set<unsigned int> get_neighbors(int i, int N)
{
std::set<unsigned int> neighbors;
if (((i % N) == 0) && (i == N*N - N))
{
// If we're on the left edge and the top left corner.
neighbors.insert(i+1);
return neighbors;
}
if (((i % N) == N-1) && (i != N*N - 1))
{
// If we're on the right edge and not the top right corner.
neighbors.insert(i+N);
return neighbors;
}
if (((i % N) == N-1) && (i == N*N - 1))
{
// If we're on the right edge and the top right corner.
return neighbors;
}
if (i >= N*(N-1))
{
// If we're on the top edge and not the top right corner (already covered
// in a previous condition).
neighbors.insert(i+1);
return neighbors;
}
else
{
neighbors.insert(i+1);
neighbors.insert(i+N);
return neighbors;
}
}
std::vector<bool> init_porous(double p, unsigned int N)
{
std::vector<bool> porous(N*N);
for (int i=0; i < N*N; ++i)
{
if ((std::rand() % 100) < (p * 100) )
{
porous[i] = true;
}
else
{
porous[i] = false;
}
}
return porous;
}
bool is_percolated(std::vector<bool> porous, unsigned int N)
{
std::set<unsigned int> neighbors;
// We need N*N+2 as we have the two virtual nodes at each end. So now the
// indices don't match porous - they're off by one.
WeightedCompressedQuickUnion WQU = WeightedCompressedQuickUnion(N*N+2);
for (int i=0; i < N*N; ++i)
{
if (porous[i])
{
if (i < N) // If the bottom row.
{
WQU.make_union(i+1, 0);
}
if (i >= N*(N-1)) // If the top row.
{
WQU.make_union(i+1, N*N+1);
}
neighbors = get_neighbors(i, N);
for (std::set<unsigned int>::iterator iter=neighbors.begin();
iter!=neighbors.end() ; ++iter)
{
if (porous[*iter])
{
WQU.make_union(i+1, *(iter)+1);
}
}
}
}
if (WQU.find(0, N*N+1))
{
return true;
}
return false;
}
int main(void) {
std::vector<unsigned int> Ns;
unsigned int MAX_TIMES = 100; // Max times to run for each p and N.
std::ofstream out;
out.open("percolation.txt");
out << "N,Porous Probability,Percolation Probability" << std::endl;
Ns.push_back(5);
Ns.push_back(10);
Ns.push_back(20);
Ns.push_back(50);
Ns.push_back(100);
for (std::vector<unsigned int>::iterator iter = Ns.begin(); iter != Ns.end();
++iter)
{
unsigned int N = *iter;
for (double p=0.01; p<1; p+=0.01)
{
unsigned int successes = 0; // Number of times percolation occurred.
for (int counter=0; counter < MAX_TIMES; ++counter)
{
std::vector<bool> porous = init_porous(p, N);
if (is_percolated(porous, N))
{
++successes;
}
}
out << N << "," << p << "," << double(successes)/MAX_TIMES << std::endl;
}
}
out.close();
return 0;
}
Monte Carlo code
#include <vector>
#include <iostream>
#include <cstdlib>
#include "unionfind.cpp"
#include <fstream>
// Get neighbors' indices for cell i in an NxN grid.
std::set<unsigned int> get_neighbors(int i, int N)
{
std::set<unsigned int> neighbors;
if (i<N)
{
// Bottom row
neighbors.insert(i+N);
if (i==0)
{
// Bottom left corner.
neighbors.insert(i+1);
return neighbors;
}
else if (i == N-1)
{
// Bottom right corner.
neighbors.insert(i-1);
return neighbors;
}
else
{
neighbors.insert(i-1);
neighbors.insert(i+1);
return neighbors;
}
}
if (i >= N*N-N)
{
// Top row
neighbors.insert(i-N);
if (i == N*N-N)
{
// Top left corner.
neighbors.insert(i+1);
return neighbors;
}
else if (i == N*N-1)
{
// Top right corner.
neighbors.insert(i-1);
return neighbors;
}
else
{
neighbors.insert(i-1);
neighbors.insert(i+1);
return neighbors;
}
}
if ((i%N) == 0)
{
// Left edge (no corners)
neighbors.insert(i+1);
neighbors.insert(i+N);
neighbors.insert(i-N);
return neighbors;
}
if ((i%N) == N-1)
{
// Right edge (no corners)
neighbors.insert(i-1);
neighbors.insert(i+N);
neighbors.insert(i-N);
return neighbors;
}
neighbors.insert(i-1);
neighbors.insert(i+1);
neighbors.insert(i+N);
neighbors.insert(i-N);
return neighbors;
}
int main(void) {
unsigned int N = 100;
unsigned int MAX_TIMES = 2000; // Max times to run for Monte Carlo
std::ofstream out;
out.open("percolation_mc.txt");
for (int counter=0; counter < MAX_TIMES; ++counter)
{
std::cout << counter << std::endl;
std::vector<bool> porous(N*N, false);
WeightedCompressedQuickUnion WQU = WeightedCompressedQuickUnion(N*N+2);
while (!WQU.find(0, N*N+1))
{
int cell = (rand() % (N*N));
// std::cout << cell << std::endl;
porous[cell] = true;
if (cell < N)
{
WQU.make_union(0, cell+1);
}
else if (cell >= N*N-N)
{
WQU.make_union(N*N+1, cell+1);
}
std::set<unsigned int> neighbors = get_neighbors(cell, N);
for (std::set<unsigned int>::iterator iter=neighbors.begin();
iter != neighbors.end(); ++iter)
{
if (porous[*iter])
{
WQU.make_union(cell+1, *(iter) + 1);
}
}
}
unsigned int transparent = 0;
for (std::vector<bool>::iterator iter=porous.begin();
iter != porous.end(); ++iter)
{
if (*iter)
{
++transparent;
}
}
out << double(transparent)/(N*N) << std::endl;
}
return 0;
}