Suppose we have \(N\) points in a plane, and we wish to find the closest pair. The brute force algorithm takes \(\Theta(N^{2})\). We can do better using divide and conquer.
Let’s split the plane into left and right halves. Then the closest pair is either entirely in one of the halves, or it is with one point in each half.
The base case is when we have very few points (say, 3) in the area under question that we can just use the brute force algorithm.
Let \(d_{L}\) be the closest pair in the left half. Define \(d_{R}\) similarly for the right half. Define \(\delta=\min\{d_{L},d_{R}\}\). The real trick is to find out if there are any pairs with a distance smaller than \(\delta\). They would necessarily have to be with a point in each half.
Before starting the whole algorithm, make two lists: One with the points sorted by \(x\) coordinate, and another with the points sorted by the \(y\) coordinate.
Note: For convenience, we assumed that the \(x\) and \(y\) coordinates are unique.
Now in the merge step, let \(x_{0}\) be the rightmost point in the left half. Construct the vertical strip centered at \(x_{0}\) and bounded by the left and right by \((x_{0}-\delta,x_{0}+\delta)\).
Now we’ll consider only points in this strip. We can easily do this by using our sorted lists. We start with the bottom-most point (lowest \(y\) coordinate), and for each point, we calculate the distances to the next 7 points higher than it in the strip. If any is less than \(\delta\), we update our smallest distance accordingly. We repeat with the next lowest point, and so on.
This scan takes at most \(O(N)\), because even though it is a double loop, one loop is bounded above by 7. The divide and conquer has at most \(\lg N\) steps. The initial sort is \(\Theta(N\lg N)\). So the complexity of this algorithm is \(\Theta(N\lg N)\).
Why 7?
7 seems like a magic number. Why do we need to look at only 7? Take a look at the following diagram:
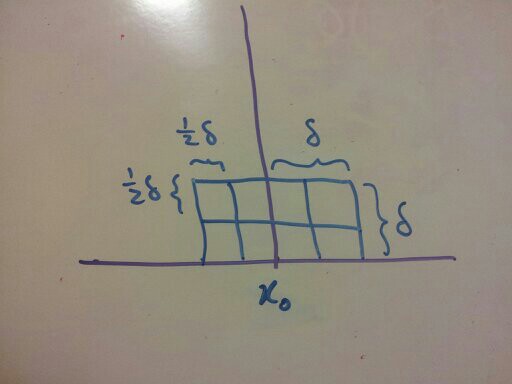
Assume we find two points with distance less than \(\delta\). Let them be \(P\) and \(Q\) with \(Q\) having the smaller \(y\) coordinate.
We’ve drawn 8 boxes, each of side length \(\frac{1}{2}\delta\), around \(x_{0}\). We align the lower side to have the same \(y\) coordinate as \(Q\).
Claim 1: \(P\) must lie in one of the 8 boxes. The proof is that the \(x\)-coordinate of \(P\) is within \(\delta\) of \(x_{0}\), and within \(\delta\) in the \(y\)-coordinate of \(Q\).
Claim 2: No two points can exist in a given box. For the proof, first note that any two points in the same box implies that they are in the same half (left or right). However, if they are in the same half, then their distance would be less than \(\delta\), which is a contradiction.
So putting the two together, we get that there are at most 7 points one needs to consider.