Dealing With Recurrence Relations

Useful Identities

\begin{equation*} \sum_{k=m}^{n}\dbinom{k}{m}=\dbinom{n+1}{m+1} \end{equation*}

The mnemonic for this is: Suppose you need to pick 4 objects from 11. We’ll partition all the ways to do this as follows: We pick the last of the 11 objects. Now we need to pick 3 more out of the remaining 10. Next, instead of picking the last element, we pick the second last element. Now we need to pick 3 items out of the 9 remaining ones (we do not want to include the last element, as all combinations involving it have been counted). And we keep iterating till we can’t go any further.

Vandermonde’s Identity

\begin{equation*} \sum_{k=0}^{r}\dbinom{m}{k}\dbinom{n}{r-k}=\dbinom{m+n}{r} \end{equation*}

Mnemonic: We have \(m\) males and \(n\) females in class. We need to pick \(r\) people from the class (no restrictions on gender). We could pick no women and all from the men. Or we could pick 1 woman and \(r-1\) men, and so on.

\begin{equation*} \sum_{m=0}^{\min(N-k,k)}\dbinom{N-k}{m}\dbinom{k-1}{m}=\dbinom{N-1}{k-1} \end{equation*}

Mnemonic: I have \(N\) integers from \(1\) to \(N\). Assume \(k\) is already in its appropriate position (the position it would be in if you sorted it). How many ways can you populate the \(k-1\) positions left of \(k\)? The RHS is the obvious answer. Another way of looking at this is: How many ways can I arrange it so that I have no entry before \(k\) that is greater than \(k?\) How about exactly one entry before \(k\) that is greater than \(k\)? And so on.

Let \(m=2\). Of the \(N-k\) integers greater than \(k\), we need to choose 2 to place before \(k\). That gives you one of the factors. Once we’ve chosen the 2, we need to choose 2 places to put it before \(k\). That gives you the other factor. Sum over all \(m\).

\begin{equation*} \sum_{k=1}^{N}k\dbinom{N}{k}=N2^{N-1} \end{equation*}

I don’t have a combinatorial proof, but we can see this by noting that \((x+1)^{N}=\sum_{k=0}^{N}\dbinom{N}{k}x^{k}\). Differentiate, then multiply by \(x\), and then set \(x=1\).

Another identity:

\begin{equation*} \dbinom{\frac{1}{2}}{k}=\frac{\left(-1\right)^{k-1}}{4^{k}(2k-1)} \end{equation*}

Obtain this by multiplying out…

Also:

\begin{equation*} \left(1+x\right)^{1/2}=\sum_{k=0}^{\infty}\dbinom{\frac{1}{2}}{k}x^{k} \end{equation*}

You can differentiate this to get the result when the power is negative, etc.

Telescoping for First Order Linear Recurrence Relations

If you have a recurrence relation of the form:

\begin{equation*} a_{n}=g(n)a_{n-1}+f(n) \end{equation*}

Then solve it via telescoping by dividing by \(\prod_{k=1}^{n}g(k)\).

\begin{equation*} \frac{a_{n}}{g(n)g(n-1)\cdots g(0)}-\frac{a_{n-1}}{g(n-1)\cdots g(0)}=\frac{f(n)}{g(n)g(n-1)\cdots g(0)} \end{equation*}

Summing all the terms yields:

\begin{equation*} \frac{a_{n}}{g(n)g(n-1)\cdots g(0)}-\frac{a_{1}}{g(0)}=\sum_{k=1}^{n}\frac{f(k)}{g(k)g(k-1)\cdots g(0)} \end{equation*}

(Not sure I got the indices correct, but the principle holds).

“Guessing” for Linear and Constant Coefficients and no Constant Term

\begin{equation*} a_{n}=c_{n-1}a_{n-1} + c_{n-2}a_{n-2}+\cdots \end{equation*}

Assume \(a_{n}=x^{n}\), substitute and solve the characteristic equation to get the solution. If you have repeated roots, then one solution is \(a_{n}=\alpha^{n}\), the other is \(a_{n}=n\alpha^{n}\), the next is \(a_{n}=n^{2}\alpha^{n}\) (in the case of multiplicity of 3).

Divide and Conquer

Binary Search

The number of compares in the worst case of binary search is:

\begin{equation*} B_{N}=B_{\lfloor N/2\rfloor}+1 \end{equation*}

To solve this, set \(N=2^{n}\) and get an exact solution for this special case (\(a_{n}=B_{2^{N}}\)).

But what if it’s not a power of 2? Then \(B_{N}\) is the number of bits in the binary representation of \(N\). We see this by realizing that it satisfies the exact same recursion relation.

Mergesort

\begin{equation*} C_{N}=C_{\lfloor N/2\rfloor}+C_{\lceil N/2\rceil} + N \end{equation*}

Can use the same trick as above, but can also do another trick by calculating \(C_{N+1}\)

\begin{equation*} C_{N+1}=C_{\lfloor (N+1)/2\rfloor}+C_{\lceil (N+1)/2\rceil}+N+1=C_{\lceil N/2\rceil}+C_{\lfloor N/2\rfloor+1}+N+1 \end{equation*}

This leads to a telescoping series.

Recursion Trees

Let \(T(n)=aT(n/b)+f(n)\). In words, we are dividing the problem into \(a\) parts, each solving the same problem of size \(n/b\). The \(f(n)\) is the cost to “combine” all the \(a\) parts.

A diagram of this process really helps:

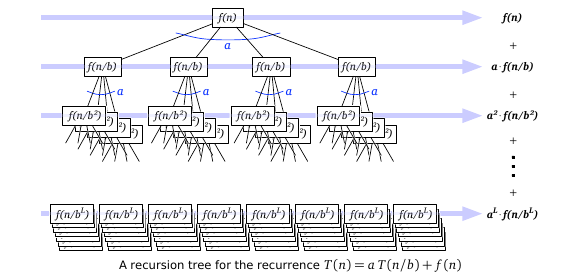
Recursion tree (courtesy of Jeff Erickson's excellent lecture notes at http://web.engr.illinois.edu/~jeffe/teaching/algorithms/)

Note that at level \(k\) of the recursion tree, we do \(a^{k}f(n/b^{k})\) work in combining.

Now the secret is that usually the base case is somewhat trivial (order \(O(1)\), although we can even loosen that bound), so we don’t really need to add it to our analysis as long as we’re interested in asymptotics. For example, the base case may have only 5 quantities. Even if the underlying base algorithm is exponential, we are limiting our “\(n\)” to 5, so it’s still \(O(1)\)!

So the total “cost” is \(T(n)=\sum_{k=0}^{L}a^{k}f(n/b^{k})\) where \(L\) is \(\log_{b}(n)\).

Often, this sum can be solved analytically.

Master Theorem

The master theorem gives a general solution to many divide and conquer algorithms.

Special Case

Suppose your algorithm divides the problem into \(a\) parts each of size \(N/b\) (both being integers). You solve the problem recursively, and then combine them. Say the cost to combine is \(\Theta\left(N^{g}\left(\log N\right)^{d}\right)\). Then the solution is

\begin{equation*} a_{n}=\Theta\left(N^{g}\left(\log N\right)^{d}\right),g>\log_{b}a \end{equation*}

\begin{equation*} a_{n}=\Theta\left(N^{g}\left(\log N\right)^{d+1}\right),g=\log_{b}a \end{equation*}

\begin{equation*} a_{n}=\Theta\left(N^{\log_{b}a}\right),g<\log_{b}a \end{equation*}

(Note that Sedgewick’s online course had the \(>\) and \(<\) signs reversed from mine, but I think mine is correct).

The master theorem requires all the subproblems to be of the same size (i.e. all of them should be of size \(N/b\).

In the theorem, we got tight bounds. This was possible as we knew our cost to combine was tight (written in \(\Theta(\cdots)\). If instead we only had the upper bound on the combine step (\(O(\cdots)\)), then the theorem is still valid, but we replace all \(\Theta\) with \(O\).

General case

A more general form of the Master’s Theorem is:

Suppose your algorithm divides the problem into \(a\) parts each of size \(n/b\) (both being integers). You solve the problem recursively, and then combine them. Say the cost to combine is \(f(n)\). Then the solution is

\begin{equation*} a_{n}=\Theta\left(f(n)\right),af(n/b)=\kappa f(n),\kappa<1 \end{equation*}

\begin{equation*} a_{n}=\Theta\left(f(n)\log_{b}(n)\right),af(n/b)=f(n) \end{equation*}

\begin{equation*} a_{n}=\Theta\left(N^{\log_{b}a}\right),af(n/b)=Kf(n),K>1 \end{equation*}

Proof of the Master Theorem

The solution is

\begin{equation*} T(n)=\sum_{k=0}^{L}a^{k}f(n/b^{k}) \end{equation*}

We can divide this sum into 3 cases:

\(af(n/b)=\kappa f(n),\kappa<1\). In words, this means that at each level of the tree, we are doing less work. Looking at the summation, this means that \(T(n)=\sum_{k=0}^{L}\kappa f(n)\) is a decreasing geometric series. Just raise the upper limit to \(\infty\) and we know the sum will simply be a constant multiplied by \(f(n)\). Hence, this is \(\Theta(f(n))\).
\(af(n/b)=\kappa f(n),\kappa>1\). In words, this means that at each level of the tree, we are doing more work. Looking at the summation, this means that \(T(n)=\sum_{k=0}^{L}\kappa f(n)\) can just be replaced by the largest term for all the terms. This will give the result.
\(af(n/b)=f(n)\). In words, this means that we do the same amount of work at each level. The result is simply \(Lf(n)\).

Note: While the master method is useful, it’s best to keep the recursion tree method in mind - it can solve problems the master method fails at. In particular, it may handle cases where not all the subproblems are of the same size.