Sample problems we want to solve:
- What are all the keys between two keys? (Relevant to databases)
- How many keys exist between two keys? (Relevant to databases)
These problems are equivalent to: Given a 1-D line with points on it, how many points fall within a specified interval?
We could use an ordered array and do a binary search. It yields the answer in \(O(\lg N)\) queries, but insertion is slow: \(O(N)\).
If we use binary search trees, we can get the results in \(O(\lg N)\) by searching for the lower and upper points in the interval, and applying the rank function.
To find all the points, use recursion:
- Given current node, look in all nodes in left subtree.
- Check the current node. If it’s not within the range, exit.
- Look in all nodes in the right subtree.
I haven’t thought this through, but I think it should work. You do need to start at a node within the range (do it by searching for the left endpoint).
The benefit of this technique is that insertion is now \(\lg N\).
Line Intersection
Assume you have multiple vertical and horizontal lines in a plane, and wish to find all the points of intersection.
Brute Force: \(O(N^{2})\) where \(N\) is the number of lines.
However, we can transform this problem into a 1-D range search problem.
Let’s see conceptually how this can be done:
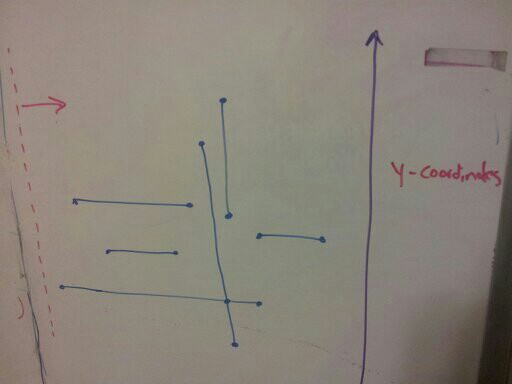
Here we have only one intersection. We sweep an invisible line (red dashes) from the left to the right. The purple line on the right represents the y-axes of the points the sweeping line encounters.
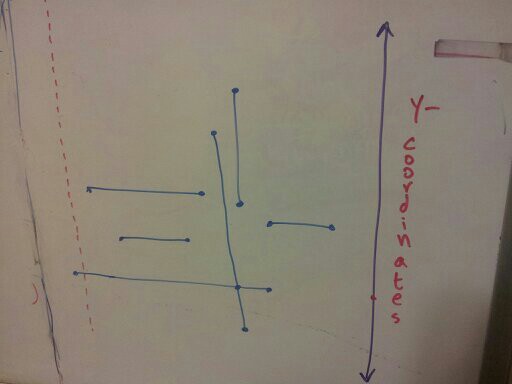
After encountering the first horizontal point, we note that this is the left endpoint. We mark it’s y-coordinate on the y-axis on the right side.
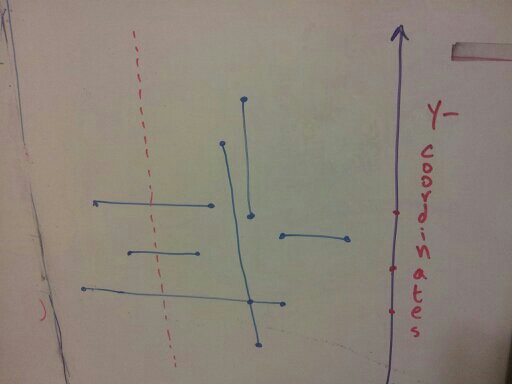
As we encounter two more horizontal line endpoints, we mark their y-coordinates as well.
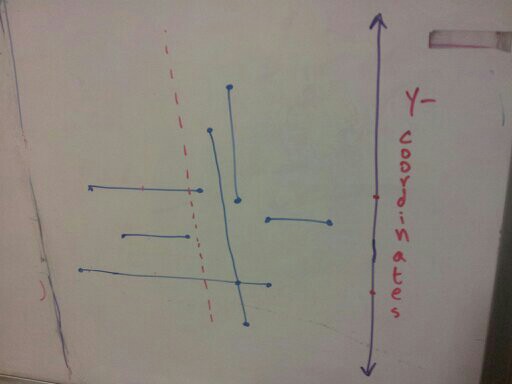
Once we meet a right end point, we’ve traversed one horizontal line, so we remove its y-coordinate from the y-axis.
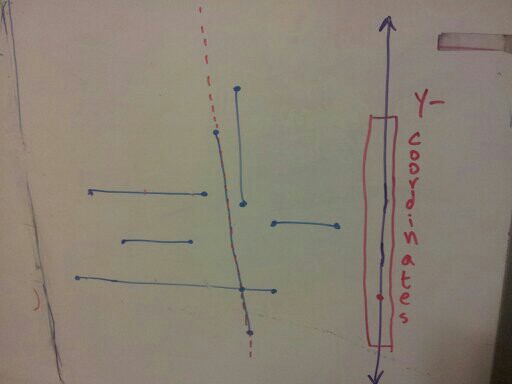
Finally, we encounter a vertical line. We look at the y-coordinates of its end points, and do a range search between them. This gives us the number of horizontal lines that intersect the vertical line.
Note that some assumptions have been made regarding the non-degeneracy of the coordinates.
Implementation
In code, we won’t need an actual sweeping line. We instead store all the end points in a binary heap sorted by x-coordinate. Each node in the heap needs to know if its a left or right endpoint (or vertical line end point).
As we pop from the binary heap, we add/remove the y-coordinate to a binary search tree as is appropriate. Then we can perform the range search as needed.
The complexity is \(O(N\lg N)\)